Gepost door Kevin van As op 23 september 2025
De nieuwe lesmodule voor keuzethema G. Algoritmiek, berekenbaarheid en logica is gepubliceerd! In dit blog leggen we je uit wat dit keuzethema allemaal omvat.
Het eerste gedeelte van de module gaat over algoritmen. Bij het oplossen van een probleem leiden meerdere wegen naar Rome, maar sommige wegen zijn een stuk sneller dan andere wegen. Om algoritmen te kunnen vergelijken op efficiëntie, bestuderen we hun groeigedrag.
Eerst meten we de looptijd van algoritmen met Python voor verschillende invoergroottes. Het groeigedrag van het algoritme kan dan zichtbaar worden gemaakt in een grafiek. Dit gedeelte van het lesmateriaal is optioneel.
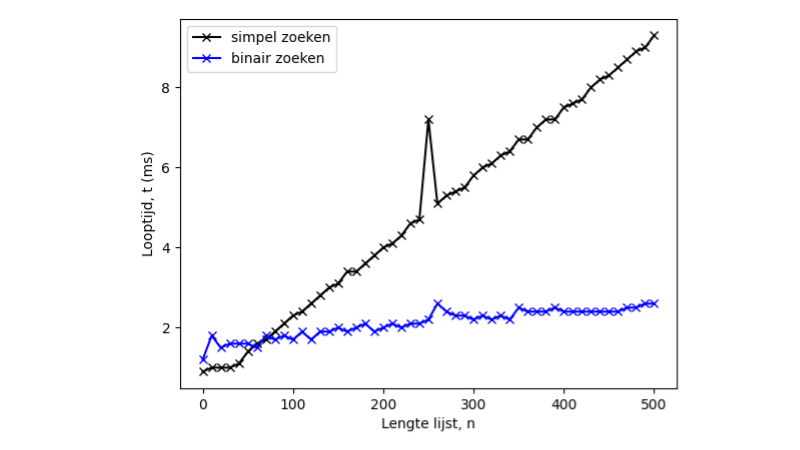
Daarna leren leerlingen hoe zij algoritmen kunnen analyseren. Door te tellen hoeveel stappen een algoritme moet zetten om de oplossing te vinden, kan bepaald worden hoe dit afhankelijk is van de grootte van de invoer. Hiermee kunnen we voorspellen wat de looptijd van het algoritme wordt bij een veel grotere invoergrootte.
Neem bijvoorbeeld het lineaire zoekalgoritme. Dit zoekalgoritme bekijkt één voor één alle elementen in een lijst, totdat het juiste element gevonden wordt. Het aantal stappen schaalt dus met de grootte van de lijst, n. Daarom vertoont dit algoritme een groeigedrag van orde O(n). Een analyse van het binaire zoekalgoritme laat zien dat dit algoritme een groeigedrag van orde O(ln n) vertoont. De logaritmische functie ln(n) groeit minder snel dan de lineaire functie n. Daarom kunnen we — zonder het algoritme uit te hoeven voeren — stellen dat het binaire zoekalgoritme efficiënter is dan het lineaire zoekalgoritme.Het groeigedrag van een algoritme zegt ook iets over de berekenbaarheid. Het lesmateriaal behandelt problemen, bijvoorbeeld het handelsreizigersprobleem, waar het groeigedrag uit de hand loopt. Dit soort problemen, die niet in een realistische tijd met de computer op te lossen zijn, noemen onhandelbare problemen. Voor dergelijke problemen moeten we benaderingen gebruiken om een redelijke oplossing in een redelijke hoeveelheid tijd te vinden.
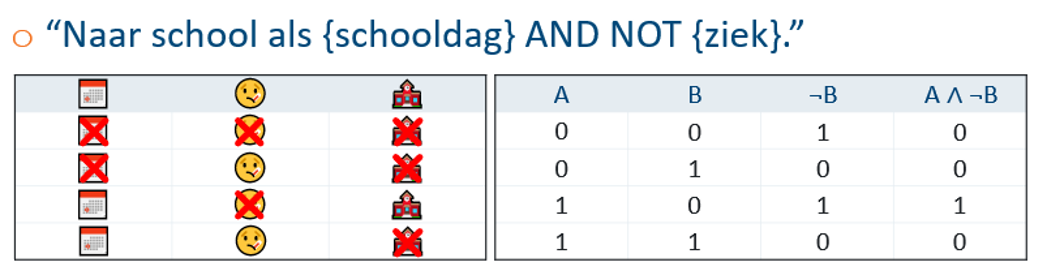
Het onderdeel logica gaat over logisch kunnen redeneren. Door wetten van de logica toe te passen, kunnen bijvoorbeeld complexe condities worden vereenvoudigd naar een vorm die beter door mensen te begrijpen is. Dit helpt om bugs in code te voorkomen.
Dit keuzethema biedt veel verbreding en verdieping op kerndomein B1. Algoritmen. De lesmodule is gebaseerd op het oorspronkelijke lesmateriaal van SLO, waar we allerlei updates op hebben uitgevoerd:
De module is vooral geschikt voor vwo-leerlingen in klas 5 of 6, maar ook gemotiveerde 5-havo-leerlingen kunnen ermee aan de slag. Programmeerkennis op basisniveau is vereist; ervaring met Python is een pre (alhoewel niet absoluut noodzakelijk).
Het onderdeel 'Paden en afstanden (G3)', bijpassend toetsmateriaal en een voorbeeldplanner zullen in het najaar worden gepubliceerd.
Deze update van het lesmateriaal is beschikbaar voor alle Fundament-gebruikers met een licentie voor de keuzethema’s. Je kunt het lesmateriaal vinden via de methode: Keuzethema's → G. Algoritmiek, berekenbaarheid en logica.
Nog niet in het bezit van een licentie voor de keuzethema’s, of een PLUS-licentie, maar wel geïnteresseerd? Onze adviseurs helpen je graag verder. Neem contact op via [email protected]!
Wanneer de werkzaamheden helemaal zijn afgerond, dan berichten we je daar natuurlijk weer uitgebreid over op onze reguliere kanalen.
-- Share It --
30/10: Bètadocentendag (Radboud)
26/3: Lerarendag van de digitale geletterdheid
