Gepost door Kevin van As op 19 november 2025
Eerder berichtten wij dat het keuzethema G. Algoritmiek, berekenbaarheid en logica voor driekwart was gepubliceerd. Het onderdeel G3. over algoritmen met de graaf-datastructuur ontbrak nog.
Nu is het moment aangebroken dat alle onderdelen gepubliceerd zijn!
Dit keuzethema biedt veel verbreding en verdieping op kerndomein B1. Algoritmen. De lesmodule is gebaseerd op het oorspronkelijke lesmateriaal van SLO, waaraan wij allerlei updates hebben uitgevoerd:
De module is vooral geschikt voor leerlingen uit 5- of-6 vwo, maar ook gemotiveerde 5-havo-leerlingen kunnen ermee aan de slag. Programmeerkennis op basisniveau is vereist; ervaring met Python is een pré (alhoewel niet absoluut noodzakelijk).
Dit keuzethema bestaat uit vier onderdelen:
In deze blog zoomen wij in op onderdelen 2 en 3 over het voorspellen van het groeigedrag van algoritmen.
Het grootste gedeelte van dit keuzethema gaat over algoritmen. Om een probleem op te lossen zijn er meerdere wegen naar Rome, maar sommige wegen naar Rome zijn toch echt een stuk sneller dan andere wegen. We willen algoritmen vergelijken op efficiëntie. Daarvoor bestuderen we het groeigedrag van algoritmen. We beginnen met het schrijven van een Python-code om de looptijd van algoritmen te meten. Hieruit zal bijvoorbeeld de volgende grafiek volgen om twee zoekalgoritmen met elkaar te vergelijken:
Het groeigedrag kunnen we ook theoretisch analyseren. Neem bijvoorbeeld het minimum-algoritme dat het kleinste getal in een lijst kan vinden. Dit algoritme groeit lineair met de grootte van de lijst, omdat we ieder getal in de lijst precies één keer moeten bekijken. We zeggen dat het groeigedrag O(n) heeft (uitspraak: “orde n”), waarbij n de grootte is van de lijst. In de informatica heet dit ook wel de computational complexity, maar voor leerlingen noemen we het “groeigedrag”.
Een ander algoritme kan een ander groeigedrag hebben. Neem bijvoorbeeld het BubbleSort-algoritme om alle getallen in een lijst te sorteren. In het worstcasescenario is de lijst in omgekeerde volgorde gesorteerd. In dit scenario moeten we (n-1) keer door de hele lijst gaan. Iedere keer dat we door de lijst gaan, zijn we (n) getallen met elkaar aan het vergelijken. Hierdoor ga je uitkomen op kwadratisch groeigedrag: O(n²).
Leerlingen moeten dergelijke analyses zelf kunnen doen. Hiermee kunnen zij vervolgens de looptijd van een algoritme bij een grotere invoergrootte inschatten. Ook kunnen zij verschillende algoritmen voor hetzelfde probleem vergelijken op efficiëntie. Hierdoor zal bijvoorbeeld blijken dat QuickSort efficiënter is dan BubbleSort in het worstcasescenario en in het averagecasescenario. Om leerlingen te helpen oefenen met het uitvoeren van dergelijke analyses, hebben wij aan het einde van onderdeel G2 zeven uiteenlopende casussen toegevoegd. Afsluitende toetsvragen kunnen bestaan uit het analyseren van een aantal bekende én onbekende algoritmen.
In het nieuwgepubliceerde onderdeel, G3. paden en afstanden, maken leerlingen kennis met een nieuwe datastructuur: de graaf. Ze leren over zoekalgoritmen in grafen, zoals Dijkstra’s algoritme om de kortste route van A naar B te vinden. Deze algoritmen analyseren wij wederom met als doel het bepalen van hun groeigedrag. Ditmaal zal het groeigedrag afhankelijk zijn van twee parameters: het aantal knopen (Engels: vertices) en het aantal zijden (Engels: edges).
Hierbij komen we ook algoritmen tegen die onhandelbaar zijn. Oftewel, algoritmen met een dusdanig stijl groeigedrag dat de oplossing niet berekenbaar is in een redelijke hoeveelheid tijd. Daarom moeten we voor dergelijke problemen algoritmen gebruiken die een redelijke oplossing benaderen, in plaats van algoritmen die de optimale oplossing vinden.
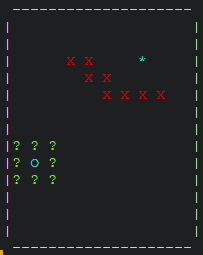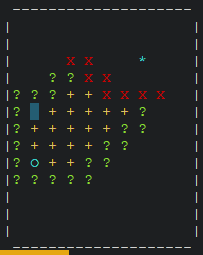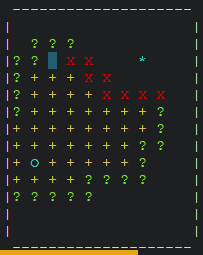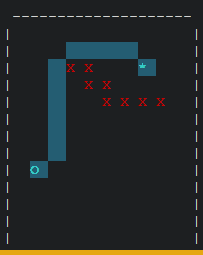
Aan het einde van onderdeel G3 staat een nieuw hoofdstuk over het A*-algoritme. Dit is een toevoeging van ons bovenop het originele SLO-materiaal. Het A*-algoritme is, net zoals Dijkstra’s algoritme, een algoritme om de kortste route van A naar B te vinden. In het averagecasescenario zal het A*-algoritme echter veel sneller zijn dan Dijkstra’s algoritme, omdat het A*-algoritme een heuristiek gebruikt om in de juiste richting te zoeken. In de volgende animatie zie je het A*-algoritme in actie:
Deze update van het lesmateriaal is beschikbaar voor alle Fundament-gebruikers met een licentie voor de keuzethema’s. Je kunt het lesmateriaal vinden via de methode: Keuzethema's > G. Algoritmiek, berekenbaarheid en logica.
Nog niet in het bezit van een licentie voor de keuzethema’s, of een PLUS-licentie, maar wel geïnteresseerd? Onze adviseurs helpen je graag verder. Neem contact op via [email protected]!
-- Share It --
7/3: Deadline aanmeldingen 3i Award
25/3: Inspiratiedag/voorjaarsconferentie informatica
26/3: Lerarendag van de digitale geletterdheid
