Gepost door Adriaan Gijssen op 31 augustus 2017

Algoritmen lijken de oplossing voor bijna alle problemen: alleen al met je smartphone maak je gebruik van heel veel geweldige algoritmen die je leven een stuk eenvoudiger maken.
Toch bestaan er eenvoudige problemen waarvoor er geen algoritme bestaat die het correct en efficiënt kan oplossen. Om leerlingen daar kennis mee te maken, introduceren we het Chinese postbodeprobleem.
Het Chinese postbodeprobleem is iets minder bekend dan het handelsreizigersprobleem, maar voor leerlingen is het herkenbaar. Je kunt het namelijk heel goed vergelijken met het lopen van een folderwijk. Daarbij moet je alle straten van de wijk aflopen. Het maakt niet uit dat je een kruispunt meerdere keren oversteekt. Je zult de folderwijk het meest efficiënt lopen als je alle straten maar één keer doorloopt. Soms is dat niet mogelijk.
Strooiwagens in de winter kennen dit probleem ook. Het is het meest efficiënt als ze alle staten maar één keer berijden. Ze zijn dan het snelst klaar.
Bij dit probleem kunnen we gebruikmaken van een gewogen graaf. In het volgende voorbeeld zijn er negen straten waar de postbode zijn post moet bezorgen. Er zijn zes kruispunten waar meerdere straten samenkomen. De getallen langs de straten geven aan hoe lang een weg is.
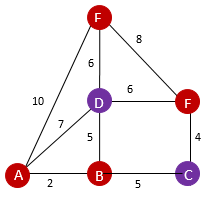
Sommige kruispunten hebben een even aantal aangesloten straten (groen: C en D). De andere hebben een oneven aantal aangesloten straten (rood: A, B, E en F). Voor het berekenen van de kortste route is de volgende stelling van toepassing:
"Als er meer dan twee kruispunten met een oneven aantal aangesloten straten zijn, moeten sommige straten meerdere keren worden doorlopen."
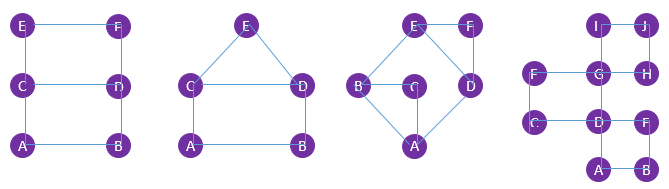
Opdracht 1
Probeer de volgende vier afbeeldingen in één keer na te tekenen. Doe dit dus zonder je potlood of pen op te tillen en zonder twee keer over dezelfde lijn te gaan.
Altijd op de hoogte blijven? Schrijf je in voor onze nieuwsbrief!